| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
Department of Chemistry, Trent University, Peterborough, Ontario, Canada K9J 7B8
A.N.Frumkin Institute of Electrochemistry, Russian Academy of Sciences, 117071 Moscow, Russia
Department of Mechanics, Royal Institute of Technology, 100 44 Stockholm, Sweden
Polarization curves for parallel electrochemical reactions of two different types for the case of no supporting electrolyte in the solution are analyzed. The consideration of the problem is based on an analytic solution, in parametric form of Nernst - Planck equations for electrodiffusion with boundary conditions of the Butler - Volmer type. It is found that the current - voltage curves for such systems clearly display the interaction of ionic components due to migration current exaltation phenomena
It is a standard electrochemical practice - to carry most experiments with sufficiently high concentration of a supporting electrolyte. Supporting electrolyte conducts the most part of electrical current at ac experiment. At relatively high concentrations of supporting electrolyte one could often neglect by the potential drop in the space between electrodes and associate the difference in electrodes' potentials with a reaction overvoltage only. That particular connivance diminishes for dc and similar to it experiments (galvanostatic, potenciostatic, polarography, etc. ), because supporting electrolyte do not conduct electrical current at dc conditions. It those experiments the supporting electrolyte is used for two main reasons. First, it minimises Joule heating in system, decreasing the overall resistance. That circumstance is especially important at limiting current density, when concentration of reagent becomes small near one of electrodes. Absence of supporting electrolyte could cause abnormal heating of electrode surface. Except for the metal electrode that could be consider as a perfect heat-conductor the local temperature disturbance could be significant that is a source for serious systematic errors in kinetic parameters estimation. Second, the supporting electrolyte suppresses migration transport of reagents and products. That circumstance is traditionally considered as a positive one. The main goal of present paper is to show a serious of situations, when study of systems with diffusion-migration transport could give us some advantage compare with conservative set-up with supporting electrolyte.
The concept of Nernst layer [1] is used widely for description of transport to the surface of electrode. It is assumed that the bulk of electrolyte is well mixed, so all concentrations are uniform everywhere except thin transport layer on the electrode surface. The thickness of transport layer, which sometimes called diffusion layer, is less then thickness of hydrodynamic boundary layer. In its turn, the later is much smaller than typical electrode size, that allows us to effectively use one-dimensional approximation of transport to the electrode surface. For the case of absence homogeneous reactions, diffusion equation gives a liner profile inside transport layer for concentrations of all component. Well-known concept of diffusion-limiting current corresponds to situation, when concentration reaches zero value at the electrode surface. Further increase of current is impossible due to transport restrictions and volt-ampere curve reaches its plate at:
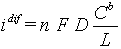 (1)
(1)
Here n - number of electrons, transferred at electrochemical reactions, F - Faraday number, D - diffusion coefficient, Cb - concentrations of reagent in the bulk of solutions, L - thickness of diffusion layer. Linear proportionally of current to the concentration of reagents is the most evident consequence of the migration transport suppression.
In the series of papers[2-14] we have consider several electrochemical systems with two simultaneous electrochemical reactions on the electrode, where both reagents and products transports by diffusion in addition to the migrations of charged ion species. The current ik transported by k-ion species is decried by Nernst-Plank equations:
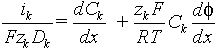 (2)
(2)
where zk is algebraic charge number, f - electric potential, x - distance, measured from electrode (0<x<L), R - gas constant, T - temperature. Equation (2) is valid only for a dilute solution only, when mobility is proportional to diffusion coefficient according with Nernst-Einstein law. For a dilute solution we assumed that concentration is equal to activity, which simplifies the model consideration significantly. Another simplification could be obtained we assuming approximately valid condition of local electroneutrality
![]() (3)
(3)
instead of exact Puason equation for electric potential and space charge density. It was shown that equation (3) gives a very good match with reality as long as thickness of diffusion layer is much greater than Debye length and no attempt to consider the phenomenon of over-limiting currents has been made.
System of differential equations (2) require values of boundary conditions for all concentrations:
Ck(L)=Ckb, f(L)=0 (4)
index "b" corresponds to known values of concentrations in the bulk solution. We assume that the thickness of diffusion layer is the same for all ions. We used as a reference value of potential its value in the bulk of solution. Now the system of differential equations (2), algebraic equation (3) and boundary conditions (4) could be formally solved. However, this solution says nothing about value of a priory unknown parameters ik. If k-ion species do not participated in the electrode reactions, its current is obviously zero: ik=0. For each electroactive ion species a separate kinetic equation should be added. Simple electrode reactions (for example, metal electrodeposition Az+ (aq) + z e- = A(s) ) are well described by Butler-Volmer equation: