| | |  |
Department of Chemistry, Trent University, Peterborough, Ontario, Canada K9J 7B8
A.N.Frumkin Institute of Electrochemistry, Russian Academy of Sciences, 117071 Moscow, Russia
Department of Mechanics, Royal Institute of Technology, 100 44 Stockholm, Sweden
Polarization curves are analyzed for parallel electrochemical reactions of two different types with no supporting electrolyte in the solution. Consideration of the problem is based on an analytic solution, in parametric form, of the Nernst - Planck equations for electrodiffusion with boundary conditions of the Butler - Volmer type. It is found that the current - voltage curves for such systems clearly display the interaction of ionic components due to the migration- current exaltation phenomena.
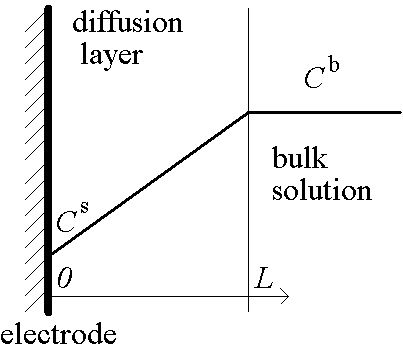
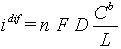
Problem statement
1) One-dimensional transport:
- spherical micro-electrodes;
- membranes.
2) Nernst-Plank equation for each ion species:
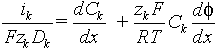
- activity coefficients are unity.
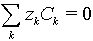
- thickness of diffusion layer is much greater than Debye length.
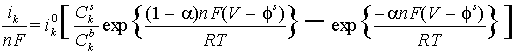
- can be solved together with the system of Nernst-Plank equations for simple electrode reaction such as Az+ (aq) + z e- ÷ ö A(s).
- For more complicated parallel reactions only the limiting current as
V6 7 could be found. The Butler-Volmer equations reduce to Cks =0.
5) Boundary conditions:
Ck(L)=Ckb, f(L)=0
(+) Arbitrary values of diffusion coefficients;
(+) Multi-charged ions;
(+) Possible homogeneous reactions in transport layer;
but
(-) the system is at steady-state;
(-) no convection;
(-) no temperature effects
(-) one electrode problem
"To solve problem" - means to find a solution to the system of differential equations and boundary conditions in a closed analytical form.
Concentration 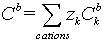 bulk concentration
bulk concentration
Potential RT/F~25 mV
Current density L / FDkCb diffusion limiting current density
Dimensionless Nernst-Plank equation:
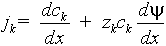
Single electrochemical reaction:
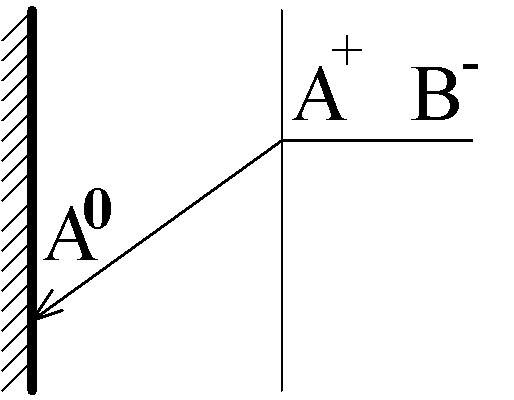
W. Nernst, Z. Phys. Chem. -1904, B.17, S.52
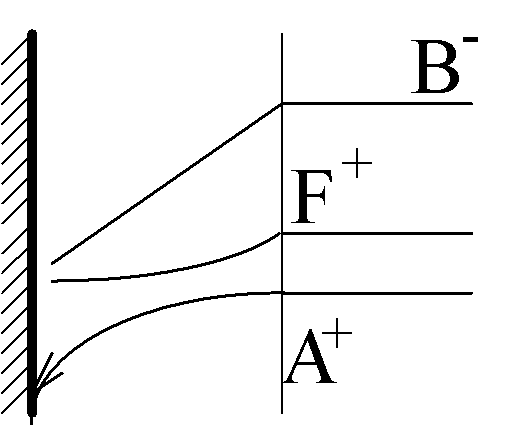
A+ + e- ÷ ö A9 .
Limiting diffusion-migration current:
jlim = 2
Binary zA-zB electrolyte:
jlim = 1+zA/zB
A. Euken, Z. Phys. Chem. -1907, B.59, S.72
Limiting diffusion-migration current:
jlim = 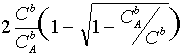
jlim 6
2 at ![]() 6 1 (binary
electrolyte)
6 1 (binary
electrolyte)
jlim 6
1 at ![]() 6 0 (large excess of
supporting electrolyte)
6 0 (large excess of
supporting electrolyte)
zA-zB electrolyte with zF-zB buffer:
L.Hsieh and J. Newman -Ind. Eng. Chem. Fund 1971, V.10, P.615.
Yu.Gurevich and Ju. Kharkats -. Sov. Electrochemistry 1979, V.15, P.94.
R. Schl` gl, Z. Phys. Chem.(Frankfurt) -1954, B.1, S.305
 For simplicity: *
zk* =1
For simplicity: *
zk* =1
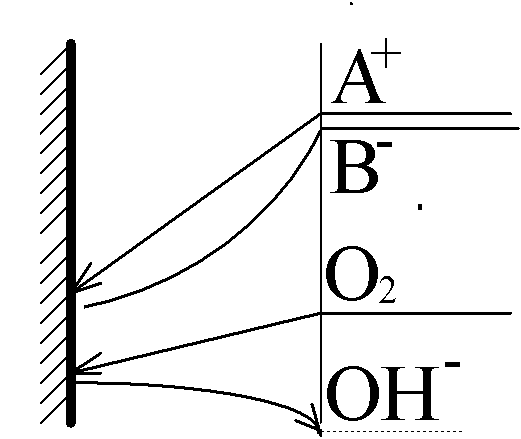
j1 is the current of the reaction in question: A+(aq) + e- ÷ ö A(s)
j0 is the current of the parallel reaction, for example:
O2(aq) + 2H2O + 4e- 6 4OH-(aq) or
O2(aq) + 2H2O + 2e- 6 H2O2(aq) + 4OH-(aq)
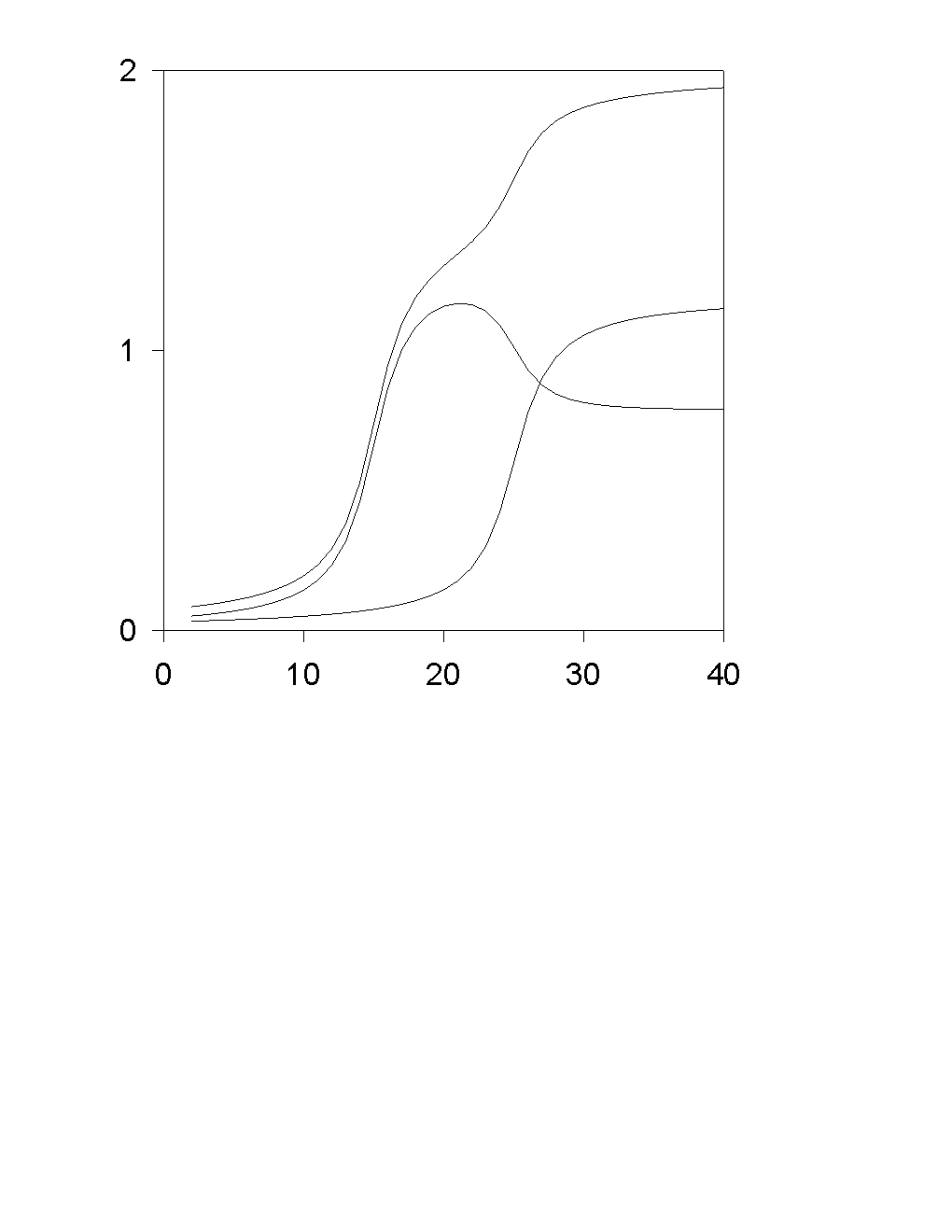
Transport of O2 occurs by ordinary diffusion, therefore j0 does not depend on j1, but the opposite it not true due to a migration interaction of A+ with OH-.
Voltamperometric curve for a=1/2:
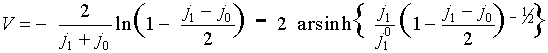
Limiting diffusion-migration current in conventional variables:
ilim = i0 + 2 i1dif + (D1/DOH) i0
For a…OQ 1/2:
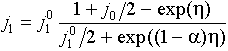
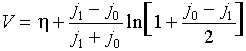
where h = V - Fs is the reaction overvoltage. The last two formulas give voltamperometric curve j1(V) in the parametric form {j1(h),V(h)}.
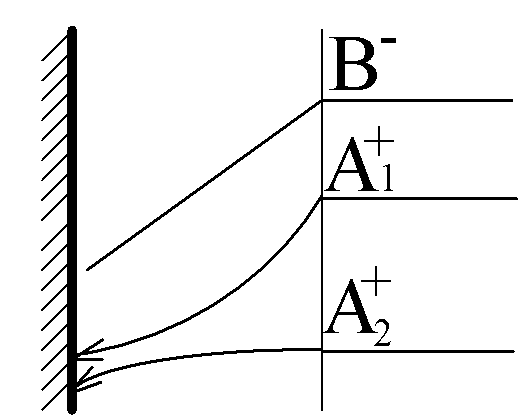 A1+(aq)+ e- ÷
ö A1(s).
A1+(aq)+ e- ÷
ö A1(s).
A2+(aq)+ e- ÷ ö A2(s)
The system of equations include three Nernst-Plank equations for A1+, A2+ and B-, as well as two Butler-Volmer equations for A1+ and A2+. This problem could be reduced to one transcendental equation.
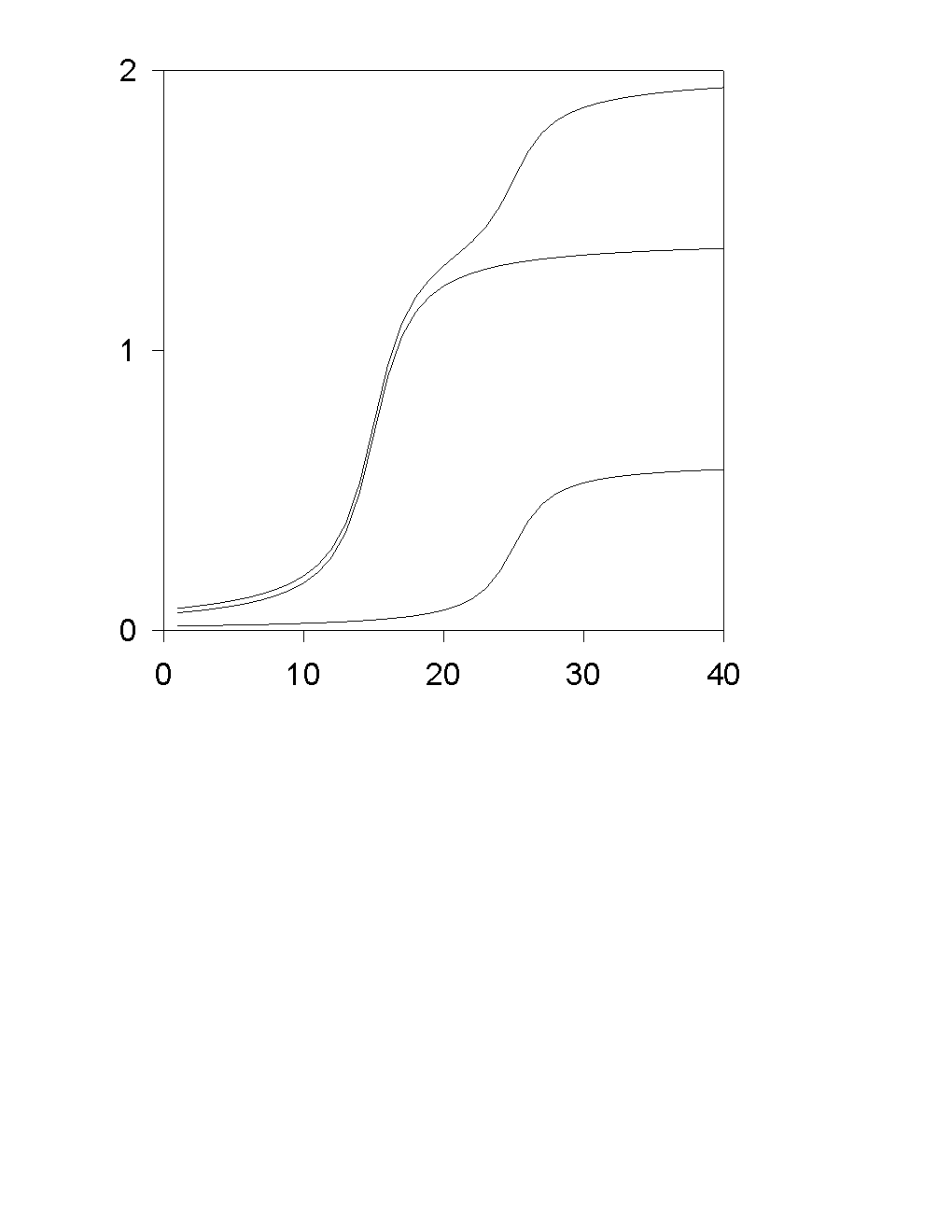
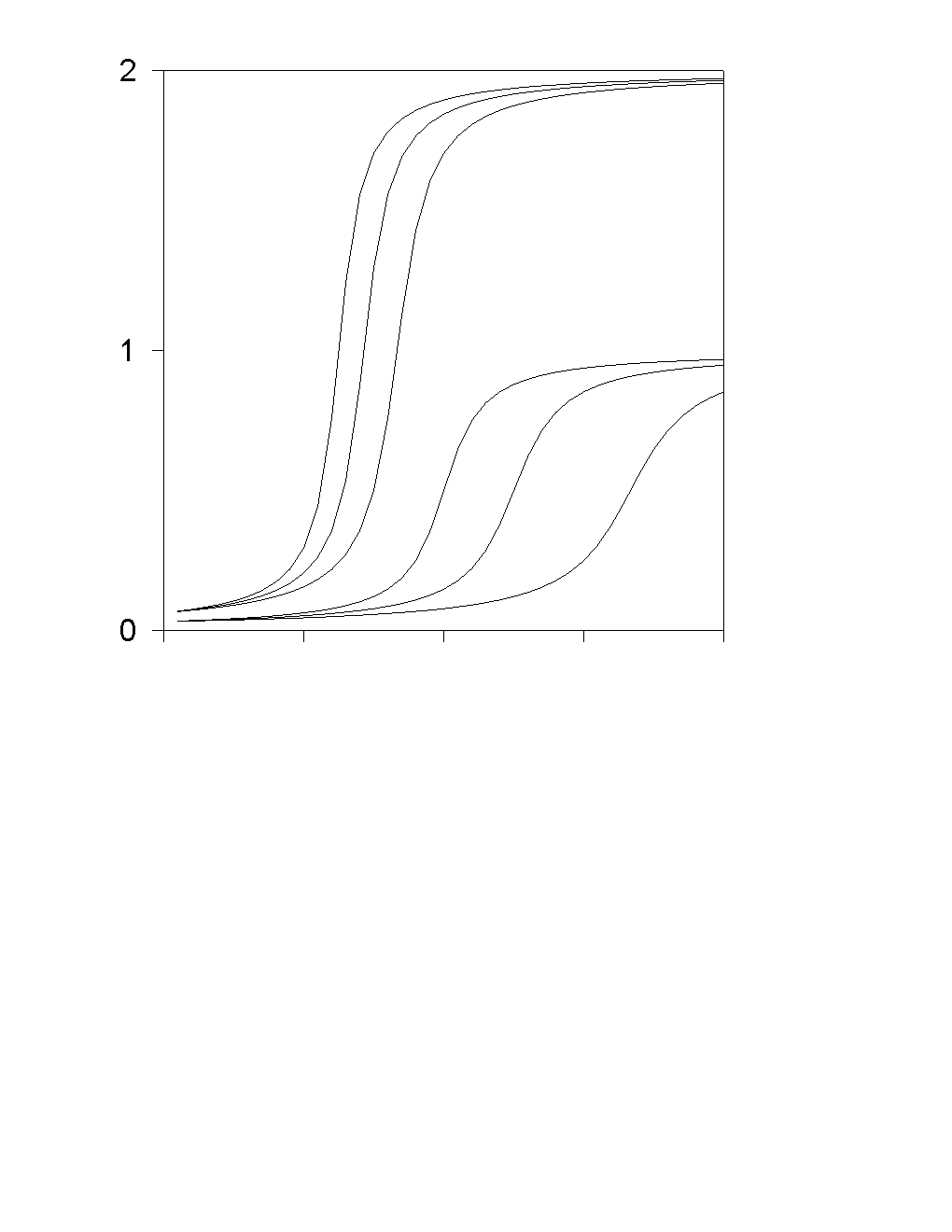 compare with
Isaak Rubinstein "Electro-Diffusion of Ions" - SIAM
1990
compare with
Isaak Rubinstein "Electro-Diffusion of Ions" - SIAM
1990
===============================================
no transport-limited current?
There are some systems with three parallel electrode reactions for which the condition of zero concentrations of all reagents Cks=0 and fast (compared to the transport) electrode kinetics are not sufficient to give a value of the current. In such situations the current depends on the relationships between the equilibrium potentials for all values of the applied potential. The whole concept of transport-limited current should be re-defined for such systems.
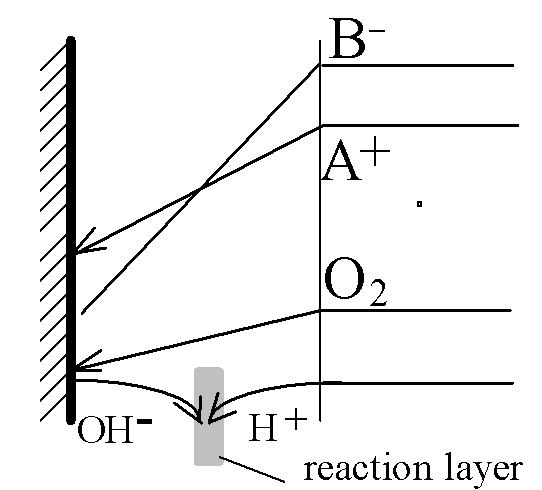
A+(aq)+ e- ÷ ö A(s).
O2 + 2H2O + 4e- 6 4OH-
OH- + H+ 6 H2O
Diffusive double-layer split into two parts:
One remains near the electrode and is responsible for the reaction kinetics - the "normal" double layer. The other, much stronger, layer moves into the region where the homogeneous reaction of water recombination takes place. It is called the "reaction double layer" and is responsible for transport limitation of the entire system.