| | |  |
| | |  |
| | |  |
| | |  |
Johan Landfors1, Daniel Simonsson1 and Artjom Sokirko2
1Department of Chemical Engineering and Technology, Division of Applied Electrochemistry and 2Department of Mechanics, Division of Hydromechanics (on leave from A.N. Frumkin Institute of Electrochemistry, Moscow, Russia)
The Royal Institute of Technology
S-10044 Stockholm, Sweden
Introduction
Mathematical modelling of the lead-acid battery is a powerful tool in the attempts to analyze, predict and optimize its performance, both in its traditional applications as a car battery for starting, lighting and ignition or as a truck battery, as well as in new applications such as uninterrupted power supply, load levelling and electric cars. Mathematical models for the lead-acid cell has been presented earlier in literature. A porous electrode model for the positive plate was extended first to the negative plate and then to the complete cell by Micka and Rousar (1). They assumed that the electrolyte between the two plates is well mixed by free convection and calculated its mean concentration from an integral material balance for the sulphuric acid. The discharge process was simulated and the discharge time was calculated as a function of plate distance. The discharge time was taken to be completed when the porosity reached 0.1 at any point. Their results showed that a certain optimum plate distance exists at which the cell capacity is highest.
A similar extension of the porous electrode models to a multi-layer cell was made by Tiedemann and Newman (2). Sunu (3) presented a one-dimensional model for a lead-acid cell consisting of a negative electrode, a porous separator, a reservoir of stagnant electrolyte and a positive electrode. The model was verified by comparison of predicted and experimentally measured cell voltage as a function of time for different discharge currents. White et.al. (4) developed a model similar to that of Sunu, which was later extended to the starved and the hermetically sealed (5,6) lead-acid cell . Recently Bernardi et. al have treated the two-dimensional case (7).
In the above papers the models were mainly used for simulating galvanostatic discharge of the cell. Recently Maja et. al. presented a model that was used for simulating fast charging of lead-acid batteries (8).
In this paper a model has been derived for a lead-acid cell consisting only of a positive and a negative electrode mechanically compressed with a porous separator inbetween them. This cell design has proved to yield a higher life under electric vehicle conditions than the ordinary starter battery type (9).
The previous models mentioned above use the transport equations for concentrated binary electrolytes. The rate equations for the charge transfer processes are generally assumed to follow an ordinary Butler-Volmer equation, and the values of the kinetic parameters have generally not been critically evaluated. The electrochemically active surface area is assumed to decrease linearly with the local extent of discharge according to relation that does not take into account the strong influence of the current density on the active mass utilization. In the present paper a special emphasis has been put on using experimentally determined kinetic equations and relations for the influence of structural changes, as well as on the experimental validation of the model. A simple method for the numerical solution of the coupled differential equations for the different regions will also be presented.
Mathematical Model
The cell investigated is schematically described in Fig.1. It consists of a porous lead dioxide electrode, a porous negative lead electrode and a porous separator region in between. This cell design with no free electrolyte between the electrodes, which are compressed with separators in between, is of interest for obtaining a long cycle life of the cell (9). In both electrodes the current is collected by a lead grid. In the cross section shown in Fig.1 only a horisontal bar of this grid is shown in each electrode.
The basic assumptions underlying the model are essentially the same as in earlier papers (2- 4). It is thus assumed that the sulphuric acid is completely dissociated into H+ and HSO4- ions, respectively. The model equations can then be derived on the basis of the transport equations for a concentrated binary electrolyte given by Newman and Tiedemann (10), with the volume-average velocity taken as the reference velocity. Calculations using e.g. Eq. (32) in Reference 10, show that the convective term can actually be neglected in the acid balances; the decrease in porosity due to the greater molar volume of lead sulphate than that of lead or lead dioxide is to a great extent compensated by the decrease in electrolyte volume due to the higher molar volume of sulphuric acid compared to water. The model equations for the three different regions are thus obtained by neglecting the convective term and applying equations (8), (11), (12), (30) and(34) in Reference (10). The equations can be written in dimensionless form by introducing the following dimensionless variables and parameters

Transport parameters with index 0 denote free electrolyte conditions.
The positive electrode, 0 £ z £ Lp/L
The material balance for sulphuric acid in the pores of the lead dioxide electrode may be written
![]()
The current balance is

The local current density varies with the overpotential according to the following Butler-Volmer equation for the electrode kinetics
![]()
where j0,p varies with the concentration
The separator, Lp/L <z < (Lp+h)/L
![]()
The equation for the current density through the separator is
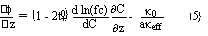
Negative electrode, (Lp+h)/L <z < 1
The material balance is analogous to that for the positive electrode
![]()
The current balance can be formulated as

The rate of the electrochemical reaction is (11)

Although the notations for transport parameters, porosity and other parameters are the same for the different regions, their values are different in the different regions.
In the equations above the electrolyte potential has been defined versus a hypothetical lead dioxide/lead sulphate reference electrode in the lead dioxide electrode and versus a lead/lead sulphate reference electrode in the separator and in the negative electrode. These different potentials are therefore defined only within their respective region. The total cell voltage can be calculated by means of Eq. (13) below.
The following initial and boundary conditions can be formulated
for t = 0: C=1, X=0, e=e0 for 0£ z£ 1 (9)
![]()


The boundary conditions in Eqs. (11) and (12) connect the concentration profiles in the three different regions. The cell voltage can be calculated by means of the following equation
![]()
![]()
This value can be found in tables. The approximate polynomial function formulated by White et. al. (5) from these data has been used in this work.
The effects of structural changes have been taken into account by means of the parameter X, the degree of discharge
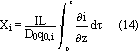
The varying porosity in the porous electrodes can be calculated as a function of X
![]()
Effective transport parameters are assumed to vary according to the following relationship, written for the effective conuctivity as an example
![]()
where li is the ratio between the effective conductivity in the active mass in its fully charged state and the conductivity in free electrolyte. k(C) is the conductivity of the free electrolyte at concentration C. A similar relation can be formulated for the effective diffusivity.
The active surface area decreases during discharge according to a relation that has borrowed its essential features from the empirical Peukert equation (11)

This relation takes into account the important fact that the electrode surface will be covered more rapidly with smaller lead sulphate crystals when the current density is higher.
The influence of the grid and its shape
The presence of the current collecting grid is difficult to take into account in the model. The grid occupies about 15-20% of the volume of the electrode. Furthermore the shape of the grid is such that its fraction eg of the vertical cross section varies linearly from zero at the exterior surface to a maximum at the midplane of the electrode, see Fig.1. An exact analysis would require a two-dimensional treatment. Here two different simplified approaches will be made, both leading to a one-dimensional analysis.
In the first case the grid cross section is taken to be rectangular, constituting a constant fraction of the plate cross-section, so that the problem becomes a truly one-dimensional one. The true geometric current density and effective transport parameters have to be calculated from the values measured with respect to the total geometric area including the grid by dividing them by the factor (1-eg), where eg is the average fraction of the vertical cross section that the lead grid occupies. In this case the theoretical charge output per unit electrode volume should be written
![]()
In the second case the macrohomogeneous approach is extended to include also the grid material in such a way that the total effective porosity in terms of electrolyte volume per electrode volume on the left hand side in the acid balances is written
e = em(1-eg). (19)
where em is the porosity of the active material. For the two different electrodes eg varies according to the following relations
![]()

![]()
![]()
The geometric current density and mass fluxes are defined with respect to the total cross-sectional area, including the grid.
The transport parameters must in this case be modified according to the following relation for the effective diffusion coefficient, compare with equation (16)
![]()
The theoretical charge output per unit electrode volume and the initial active surface area also vary along the depth of the electrode:
![]()
![]()
Input parameters are given in Table 1. Values of the transport parameters in free electrolyte have been taken from literature. The mean activity coefficient for the sulphuric acid dissociated as a binary electrolyte, has been calculated from a correlation of data for the mean activity coefficient of hydrogen and sulphate ions at complete dissociation of sulphuric acid (12). The conductivity and diffusivity of 5.0 M sulphuric acid were taken from values given for 25 oC in (4), which were recalculated to 23 oC using the equations for temperature dependence of these parameters given in the same paper.
Numerical Procedure
In order to solve the coupled differential equations for the multiple region system representing the lead-acid cell above an efficient numerical method is required. Using a finite difference method with second order accuracy the interior boundary conditions will generally lead to a jacobian coefficient matrix with rows corresponding to these boundary conditions which has five elements instead of three. White et. al. have therefore solved these equations with a pentadiagonal BAND(J) method (5,6). They have also presented a modification of the BAND(J) method for these types of problems called MBAND(14). In this work another and simplifying method has been used. The mesh for discretization according to the finite difference method has been chosen so that all boundaries are midway between two neighbouring mesh points. Introducing image points in the ordinary way for the extension of the different regions and then eliminating these points, by applying the boundary condition and the condition of continuity, will lead to a threediagonal coefficient matrix for the whole multi-region system. The coupled differential equations for the concentration and the overvoltage can then be solved can then be solved by the ordinary BAND(J) method.
Artjom ............
Experimental
The electrodes used in this study were commercially available pasted electrodes for SLI-batteries manufactured by TUDOR AB in Nol, Sweden. The full size dimensions were 115x155 mm with thicknesses of approximately 1.7 and 1.9 mm for the lead and the lead dioxide electrodes respectively. The current collector grids were made of a lead alloy with 2.5 % Sb. Experiments were performed on electrode samples that had been cut out from the full size plates to about 51 mm in height and 34 mm in width. The samples were taken both from the upper and the lower parts of the plates, so that one side of each electrode sample consisted of the grid bar to which a 3 mm lead rod was welded as current collector.
The electrolyte during the preparative cycling and before discharge experiments was in all cases 5.05 M sulphuric acid prepared from 98 % acid (Merck, pro analysi) and purified water from a combined Milli-RO 15 and Milli-Q Water Purification system from Millipore. The concentrations were determined by acid-base titrations and/or refractive index measurements. (Handbook of Chemistry and Physics).
Lead and lead dioxide electrodes were precycled in pairs in glass beakers with the electrodes separated by a microporous separator to avoid short circuiting. The electrodes were allowed to soak in the electrolyte for about one hour before they were automatically cycled at a constant current density of 100 Am-2 according to the following scheme:
1. Charge to oxygen evolution.
2. Resting period for 3600 s.
3. Discharge for 14605 s, corresponding to approximately 80 % depth of discharge
at rated capacity in the cell.
4. Resting period for 3600 s.
5. Recharge for 17526 s, corresponding to 20 % overcharge,
6. Steps 2 to 5 were repeated in total three times.
After the preparative cycling, the electrolyte in the beakers was changed to ensure a concentration of 5.05 M. The beakers, with electrolyte and electrodes, were placed under vacuum maintained by a water jet for a period of at least 10 hours. This was done to remove as much as possible of the gas in the porous electrodes and replace it with electrolyte. After evacuation, the electrolyte was changed once again. The temperature during the discharge experiments was 23oC.
The prepared electrodes were mounted into an experimental cell of which a schematic drawing is shown in Fig. 2. The cell consisted of two thick endplates made of PTFE with a U-formed distance made of PMMA that formed a well defined cell. The total distance over the electrodes then became exactly 7.0 mm. The height and the width of the cell matched the form and dimensions of the electrodes. In each end block there was a hole perpendicular to the electrode surface. The hole was used to measure the electrode potential at the rear of each electrode by Hg/Hg2SO4 reference electrodes in saturated K2SO4 manufactured by Radiometer. Three glass fibre separators (BG 200 17 by Hollingsworth and Vose) with the same dimensions as the electrodes were placed between the electrodes. The separators were immersed in sulphuric acid and evacuated in the same way as the electrodes. A Mechanical pressure was applied perpendicular to the electrode plates to seal the cell and to get a well defined electrode distance. Any free acid, i. e. acid that was not soaked by the electrodes or the separator, was removed from the cell container with a syringe. This set-up defined the cell at time equal to zero.
The cell was then galvanostatically discharged at different current densities from 100 to 1000 Am-2. During discharge, the cell voltage and the electrode potentials at the rear of the electrodes were measured on x-t recorders. The discharge was stopped at a cell voltage of 1V. The cell was then immediately disassembled. The remaining amount of sulphuric acid was then separately leached out from each cell component by soaking in multiple small portions of purified water until the leaching water was neutral. The amount of acid in each cell component could then be determined by an acid-base titration. Some cells were disassembled without discharge in order to determine the porosity of the electrodes and the separators. The concentration profiles in the cells after discharge could thus be calculated by comparing the initial amount of acid with that found after discharge and compensating for the change in porosity due to the formation of lead sulphate from lead and lead dioxide, respectively.
The distribution of lead sulphate along the thickness of the electrodes was determined with an electron probe micro analyser (ARL SEMQ 42) by recording the S-Ka radiation. The electrodes for sulphate analyses were leached in acetone instead of water. The electrodes were then dried at 50 oC and representative samples from the central part of the electrodes were taken out. The samples were then moulded into an epoxy resin under vacuum, polished with diamond paste and sputtered with a conductive layer of carbon before the analyses.
Results and Discussion
The computer program was first tested with the model and input parameters used by Nguyen and White in (6). The results obtained were in good agreement with those of Fig.2 in (4).
The effect of the parameter Ka´ is shown in Fig. ( ). A larger value of this parameter means a higher possible utilization of the active electrode material and therefore a higher discharge capacity.
Fig. ? shows the effect of separator porosity on the discharge capacity. It can be seen that this parameter has a marked influence on the discharge capacity, since at given dimensions of the different regions a higher separator porosity means both a higher effective diffusivity and a larger amount of stored acid. This parameter is therefore of great importance for a cell design of the type described in Fig.1. For high rates of discharge the higher effective diffusivity is the most important factor, since the electrolyte in the separator is consumed only to a lesser extent, while at low rates of discharge the amount of electrolyte in the separator may become a limiting factor. With the actual cell design it is not meaningful to use an extra electrolyte volume above the electrodes, since free convection is practically fully eliminitated in this case. In order to have a sufficient amount of electrolyte for low rate discharges, the separator region must be made thicker and the ohmic potential drop therefore also increases.
A comparison between the two different ways to take into account the influence of the current collector grid is shown in Fig. ?. The difference between the two cases is mainly that ....
An important aim of this study was to validate the model by comparing results predicted by the model with those obtained experimentally. Calculated and measured concentration profiles at different current densities are shown in Figs. ( ). The agreement is ......
Calculated and measured voltage-time curves are shown in Fig. ( ). The prediction of the time for a complete discharge is in ??? agreement with the experimental value. The cell voltage .........
Conclusions
Acknowledgments
This work was financially supported by the Swedish National Board for Industrial and Technical Development. We also thank Tudor AB in Nol, Sweden for their supply of electrodes to the experimental program.
References
1. K. Micka and I. Rousar, Electrochim. Acta 21, 599 (1976).
2. W.H. Tiedemann and J. Newman, in "Battery Design and Optimization", S. Gross, Editor,
p. 23, The Electrochemical Society Softbound Proceedings Series, Princeton, NJ (1979)
3. W.G. Sunu, in "Electrochemical Cell Design", R.E. White, Editor, p. 357, Plenum Press,
New York (1984)
4. Hiram Gu, T.V. Nguyen and R.E.White, J. Electrochem. Soc. 134, 2953 (1987).
5. T.V. Nguyen, R.E.White and Hiram Gu, J. Electrochem. Soc. 137, 2998 (1990)
6. T.V. Nguyen and R.E.White, Electrochim. Acta, 38, 935 (1993)
7. Dawn M. Bernardi, Hiram Gu and Andrew Y. Schoene, J. Electrochem. Soc. 140, 2250 (1993).
8. M. Maja, G. Morello and P. Spinelli, J. Power Sources, 40, 81 (1992)
9. Johan Landfors, to be published
10. John Newman and William Tiedemann, AIChE Journal, 21, 25 (1975)
11. P. Ekdunge and D. Simonsson, J. Appl. Electrochem., 19, 136 (1989)
12. K. Micka and I. Rousar, Electrochim. Acta, 18, 629 (1973)
13. D. Simonsson, J. Appl. Electrochem., 3, 261 (1973)
14. D. Fan and R.E. White, J. Electrochem. Soc., 138, 1688 (1991)
Figure Captions
Fig. 1 Schematic drawing of the cell showing the three different regions
Fig. 2 The cell used during discharge experiments. (Johan)
Table 1. Values of the parameters used in the calculations. Temperature = 23?oC.
------------------------------------------------------------------------------
Parameter Value or expression Ref.
------------------------------------------------------------------------------
c0 5.0 mol dm-3
D0 2.9 10-9 m2/s (4)
Dc/D0 0.706 + 0.294 C (13)
ki (Vp - Vr)/Vr,i
L, Lp, h, L
![]() (12)
(12)
![]()
t+0 0.8224 - 0.0725 C - 0.0302 C2
S0j00 1740 (p), 1.9 105 (n) A/m3 (?, 11)
jclim
Vp,p, Vp,n 48.9 10-3 m3 kmol-1 (13)
Vr,p 25.5 10-3 m3 kmol-1 (13)
Vr,n 25.5 10-3 m3 kmol-1 (13)
lp 0.22 Measured
ln 0.33 "
ls varies according to Figs
n 1.35 (p), 1.4 (n)
ac p: 1.5 (2?) n: 0.9 JL, DS ev Jean V? (Fig!)
eg 0.17 (average) measured
e0 0.58 (p), 0.60 (n OBS!) measured
k0 76 W-1 (4)
k k0(0.20 + 2.1 C - 1.3 C2) (0.2≤C≤1) (13)
k0 2.84 C (0≤C<0.2)
